Boyer-Moore算法,由德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授在1977年提出,因效率之高而被应用在文本编辑器的查找功能中。
BM算法基于Pattern从右到左匹配,但Pattern的整体还是从左到右移动的,可以说是对BF(Brute Force)算法的改进,BF算法的实现如下:
function bf (text, pattern) {
const txtLen = text.length
const ptnLen = pattern.length
const res = []
for (let i = 0; i < txtLen; i ++) {
for (let j = 0; j < ptnLen; j ++) {
if (text[i + j] !== pattern[j]) {
break
} else if (j === ptnLen - 1) {
res.push(i)
}
}
}
return res
}

BF算法非常简单粗暴,就是将Pattern从左往右匹配,遇到不相等就把Pattern向右移动一位,再从左往右匹配,不断重复,直到Pattern不能移动为止,因此该算法通常被称为暴力算法。BM算法定义了两条规则:坏字符和好后缀,解决BF算法中遇到字符不匹配时Pattern只能移动一位的问题,使得效率大大提高。
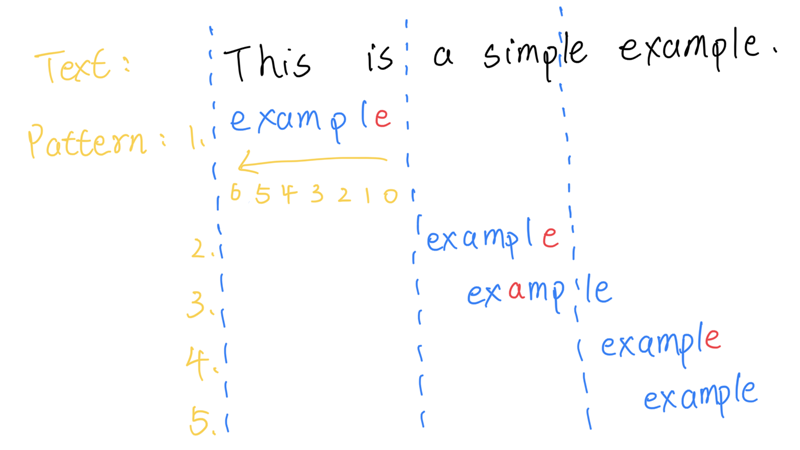
坏字符规则
Text和Pattern的字符不相等时,Text中不相等的字符被称为坏字符,坏字符分两种情况:
- 不在
Pattern中:整体移动Pattern的长度 减去 已匹配的位数; - 在
Pattern中:整体移动 该字符在Pattern中最后出现的位置到尾部的距离 减去 已匹配的位数;
如上图所示,在第一轮的第一个字符匹配中,s和e不相等,那么s就是坏字符,由于s不在example中,因此移动的位数为:example的长度(7) – 已匹配的位数(0) = 7;
第二轮的第一个字符匹配中,p和e不相等,坏字符p存在于example中,那么移动的位数则为:p在example中最后出现的位置到尾部的距离(2) – 已匹配的位数(0) = 2。
先用一个对象记录Pattern中每个字母最后出现的位置到尾部的距离:
function bm (text, pattern) {
const txtLen = text.length
const ptnLen = pattern.length
const ptnLast = ptnLen - 1
/**
* 构建Pattern的字符表,记录每个字符到尾部的距离
* example: {'e':0, 'x':5, 'a':4, 'm':3, 'p':2, 'l':1}
*/
const badChar = {}
for (let i = 0; i < ptnLen; i ++) {
badChar[pattern[i]] = ptnLast - i
}
}
该规则会出现Pattern倒退的情况,如果将上图的simple改为semple,则在第三轮的第五个字符匹配中,e和a不相等,e在example中最后出现的位置(0) – 已匹配的位数(4) = -4,这个时候需要结合好后缀规则使用。
好后缀规则
已匹配成功的后缀被称为好后缀,还是上面那张图,第三轮的匹配中mple就是好后缀,而ple、le、e是好后缀子串。好后缀规则有三种情况:
Pattern子串出现过好后缀,整体移动 子串到好后缀的距离;- 如果上面条件不成立,则需要在好后缀中寻找能够与前缀匹配的子串,整体移动 前缀到好后缀子串的距离;
- 如果上述条件均不成立,则整体移动
Pattern的长度。

用一个数组记录Pattern子串中的好后缀跳转表,另一个数组记录后缀子串能否与前缀匹配:
function bm (text, pattern) {
// ...
/**
* 构建好后缀跳转表和前缀匹配表
* example: [0, 0, 0, 0, 0, 0, 6] [false, false, false, false, false, false, true]
*/
const suffixes = Array(ptnLen).fill(0)
const prefixes = Array(ptnLen).fill(false)
for (let i = 0, len = ptnLast - 1; i < len; i ++) {
let start = i // 前面的索引
let offset = ptnLast // 后面的索引
while (start >= 0 && pattern[start] === pattern[offset]) {
if (suffixes[offset] === 0) suffixes[offset] = offset - start
start --
offset --
}
if (start === -1) prefixes[offset + 1] = true
}
}
开始匹配
Pattern从右向左匹配,若全部匹配成功就将当前索引添加到结果集合中,否则获取坏字符和好后缀规则的移动位数,将Pattern整体向右移动两个移动位数之间的最大值。
function bm (text, pattern) {
// ...
/**
* 整体从左向右移动
*/
const res = [] // 结果集合
let start = 0 // 开始位置
const end = txtLen - ptnLen // 结束位置
while (start <= end) {
// pattern从右到左匹配
let offset = ptnLast
while (offset >= 0 && pattern[offset] === text[start + offset]) {
offset --
}
if (offset < 0) {
// offset小于0说明pattern被匹配成功
res.push(start)
start += ptnLen
} else {
// 获取坏字符规则移动位数
const badSkip = (characters[text[start + offset]] === undefined ? ptnLen : characters[text[start + offset]]) - (ptnLast - offset)
// 获取好后缀规则移动位数
const goodSkip = offset === ptnLast
? 0
: (() => {
if (suffixes[offset + 1] !== 0) return suffixes[offset + 1]
for (let i = offset + 2; i < ptnLast; i ++) if (prefixes[i]) return i
return ptnLen
})()
// pattern整体向右移动坏字符和好后缀的最大值
start += Math.max(badSkip, goodSkip)
}
}
return res
}
性能测试
在不同字数的文本中查找某个单词:
| 单词个数 | BF算法 | BM算法 |
| 50 | 0.30ms | 0.40ms |
| 500 | 0.52ms | 0.46ms |
| 5000 | 3.50ms | 1.70ms |
可以看到,由于BM算法需要在匹配前进行预处理,单词个数较少的情况下效率可能不如BF算法,但是单词个数越多,效率体现的就越明显。
当然,在实际开发时还是原生方法更香…
哟哟哟,这不summy杨吗,几天不见,这么拉了
?